İçerik

• adımlar
• İpuçları

Matematikçiler ve grafik programcıları genellikle iki vektör arasındaki açıyı bulmaya ihtiyaç duyar. Neyse ki, bu açıyı hesaplamak için kullanılan formül, basit bir skaler üründen başka bir şey gerektirmez. İki boyutlu vektörleri kullanırken bu formülün arkasındaki mantığı anlamak daha kolay olsa da, herhangi bir sayıda bileşene sahip vektörlere kolayca uyarlayabiliriz.

adımlar

Bölüm 1/2: İki vektör arasındaki açıyı hesaplayın

1. 

   İki vektörü tanımlayın. İki vektör hakkında bilinen tüm bilgileri not edin. Bu eğitimin amacı doğrultusunda, vektörleri yalnızca boyutsal koordinatları açısından bildiğinizi varsayacağız (aynı zamanda bileşenler). Zaten biliyorsanız modül veya standart Bu vektörlerden (yani uzunlukları), aşağıdaki adımlardan bazılarını atlayabilirsiniz.
   • Örnek: İki boyutlu vektörleri = (2,2) ve = (0,3) olarak ele alacağız. Bu iki vektör, = 2 olarak yeniden yazılabilirben + 2j e = 0ben + 3j = 3j.
   • Örneğimiz iki boyutlu iki vektör kullansa da, aşağıdaki talimatları herhangi bir sayıda bileşene sahip vektörlere uygulayabiliriz.

2. 

   
   
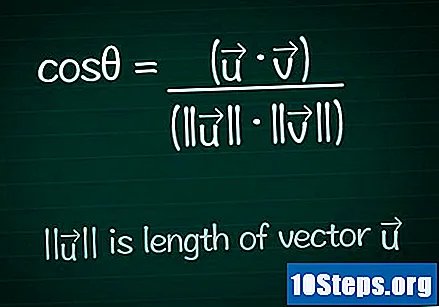
   Kosinüs formülünü yazın. Herhangi iki vektör arasındaki θ açısının değerini bulmak için, önce o açının kosinüsünü hesaplamalıyız. Formülü ayrıntılı olarak arayabilir ve bulabilir veya aşağıdaki gibi yazabilirsiniz:
   • cosθ = (•) / (|||| ||||)
   • |||| temsil etmek modül (veya vektörün uzunluğu) ".
   • • temsil etmek skaler çarpım (veya iki vektörün dahili çarpımı).

3. 

   
   
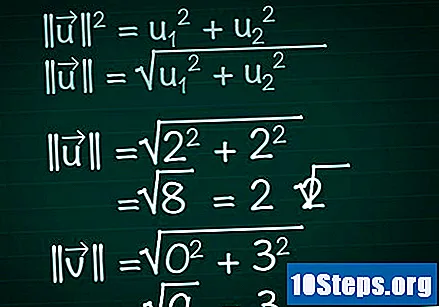
   Her vektörün modülünü hesaplayın. Bileşenin oluşturduğu bir dik üçgen hayal edin x bir vektörün bileşeni y ve vektörün kendisi. Bu üçgende vektör hipotenüsün rolünü oynar; bu nedenle, uzunluğunu bulmak için Pisagor teoremini uygulayacağız. Sonuç olarak, bu formül herhangi bir sayıda bileşene sahip vektörlere kolayca uygulanabilir.
   • || u || = u₁ + u₂. Vektörün ikiden fazla bileşeni varsa, + u eklemeye devam edin₃ + u₄ +...
   • Bu nedenle, iki boyutlu bir vektör için yapmamız gerekecek || u || = √ (u₁ + u₂).
   • Örneğimizde, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   İki vektör arasındaki skaler çarpımı hesaplayın. Vektörleri çarpma yöntemini zaten biliyor olmalısınız, aynı zamanda skaler çarpım. İki vektörün skaler çarpımını bileşenleri cinsinden hesaplamak için, bileşenleri aynı yönde birbirleriyle çarpıyoruz ve sonra bu ürünlerin sonuçlarını ekliyoruz.
   • Bilgisayar grafik programlarıyla çalışıyorsanız, devam etmeden önce ilk olarak "İpuçları" bölümünü ziyaret edin.
   • Matematiksel terimlerle, • = u₁v₁ + u₂v₂, burada u = (u₁sen₂). Vektörünüzün ikiden fazla bileşeni varsa, + u eklemeye devam edin₃v₃ + u₄v₄...
   • Örneğimizde, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Bu, ve vektörleri arasındaki skaler çarpımın değeridir.

5. 

   Bu sonuçları kosinüs formülünde değiştirin. Unutmayın, cosθ = (•) / (|||| || ||). İki vektörün skaler çarpımını ve modülünü zaten hesaplamıştık. Şimdi formüldeki bu değerleri değiştirelim ve açının kosinüsünü hesaplayalım.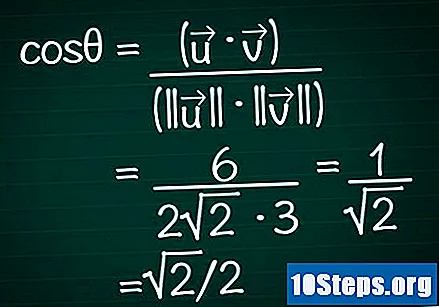
   • Örneğimizde, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Açıyı kosinüsünüze göre bulun.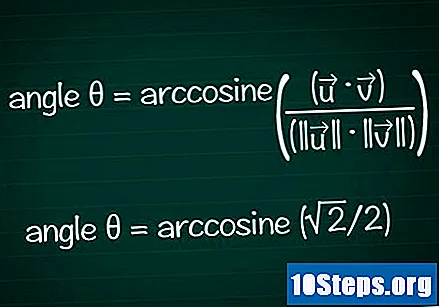
   Kosinüs değerinizden θ açısını belirlemek için hesap makinenizin yay veya cos işlevini kullanın. Bazı durumlarda, açı değerini birim daireye göre bulmanız mümkün olabilir.
   • Örneğimizde, cosθ = √2 / 2. Açıyı bulmak için hesap makinenize "arccos (√2 ​​/ 2)" yazın. Diğer bir seçenek, cosθ = √2 / 2 olan birim çemberin θ açısını aramaktır: bu, θ = /₄ veya 45 °.
   • Tüm bilgileri bir araya getirerek, son formülü elde edeceğiz θ = arccosine ((•) / (|||| ||))

Bölüm 2/2: Açıyı hesaplamak için formül tanımlama

1. 

   Formülün amacını anlayın. İki vektör arasındaki açıyı hesaplamak için kullandığımız formül önceden var olan kurallardan türetilmedi; bunun yerine, iki vektör arasındaki skaler çarpımın ve aralarındaki açının bir tanımı olarak oluşturuldu. Ancak bu karar keyfi değildir. Temel geometriye daha yakından baktığımızda, bu formülün neden bu kadar kullanışlı ve sezgisel tanımlarla sonuçlandığını görebiliriz.
   • Aşağıdaki örnekler, çalışmak için en sezgisel tip oldukları için iki boyutlu vektörlerden yararlanmaktadır. Üç veya daha fazla boyutlu vektörlerin özellikleri genel formülden tanımlanır (yine çok benzer şekilde).

2. 

   Kosinüs yasasını gözden geçirin. Herhangi bir üçgende, kenarların oluşturduğu θ açısını düşünün ve B ve yan ç bu açının karşısında. Kosinüs yasasına göre, c = a + b -2abkemer(Θ). Bu formülün gösterimi, temel geometri bilgisinden kolayca elde edilebilir.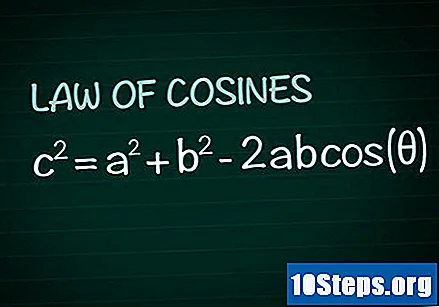

3. 

   Bir üçgen oluşturmak için iki vektörü birleştirin. Aralarında Draw açısıyla bir çift vektör çizin. Ardından, bir üçgen oluşturmak için aralarına üçüncü bir vektör çizin. Başka bir deyişle, vektörü + = veya basitçe = - olacak şekilde çizin.

4. 

   Kosinüs yasasını bu üçgene uygulayın. Yanlarımızın uzunluğunu değiştirin vektör üçgen (yani, vektör modülü) kosinüs yasası formülünde:
   • || (a - b) || = || a || + || b || - 2 || bir || || b ||kemer(θ)

5. 

   Formülü skaler ürünleri kullanarak yeniden yazın. İç çarpımın, diğerine yansıtılan bir vektörün genişlemesi olduğunu unutmayın. Bir vektörün skaler çarpımı, yönde bir değişiklik olmadığı için projeksiyon gerektirmez. Bu, • = || a || olduğu anlamına gelir. Bu bilgilere dayanarak, kosinüs yasasının denklemini yeniden yazalım:
   • (-) • (-) = • + • - 2 || a || || b ||kemer(θ)

6. 

   Formülü basitleştirin. Denklemin sol tarafındaki ürünleri genişletin ve ardından açıları hesaplamak için bildiğimiz formüle ulaşıncaya kadar basitleştirin.
   • • - • - • + • = • + • - 2 || a || || b ||kemer(θ)
   • - • - • = -2 || a || || b ||kemer(θ)
   • -2 (•) = -2 || a || || b ||kemer(θ)
   • • = || a || || b ||kemer(θ)

İpuçları

• Hızlı çözüm için aşağıdaki formülü herhangi bir iki boyutlu vektör çiftine uygulayın: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Bilgisayar grafik programlarıyla çalışıyorsanız, büyük olasılıkla vektörlerin uzunluklarını değil, yalnızca yönlerini bilmeniz gerekecektir. Denklemleri basitleştirmek ve programınızı hızlandırmak için aşağıdaki adımları izleyin:
  • Her vektörü normalleştirin, yani orijinal vektörle aynı yöne sahip birim vektörü bulun. Bunu yapmak için, vektörün her bir bileşenini vektör modülüne bölün.
  • Orijinal vektörlerin değil normalleştirilmiş vektörlerin skaler ürününü hesaplayın.
  • Normalleştirilmiş vektörlerin modülü (yani uzunluk) üniter olduğu için, onları formülün dışında bırakabiliriz. Açıları hesaplamak için son denkleminiz yaylar (•) olacaktır.
• Kosinüs yasasının formülüne dayanarak, söz konusu açının keskin mi yoksa geniş mi olduğunu hızlı bir şekilde bulabiliriz. Cosθ = (•) / (|||| ||||) ile başlayın:
  • Denklemin sol ve sağ tarafları aynı işarete sahip olmalıdır (pozitif veya negatif).
  • Uzunluklar her zaman pozitif olduğundan, cosθ her zaman skaler çarpım ile aynı işarete sahip olacaktır.
  • Bu nedenle, skaler çarpım pozitifse, cos positive pozitif olacaktır. Bu, açının birim çemberin ilk çeyreğinde, yani θ <π / 2 veya 90 ° olduğu anlamına gelir. Bu nedenle açı akuttur.
  • Skaler çarpım negatifse, cosθ negatiftir. Bu, açının birim çemberin ikinci çeyreğinde olduğu anlamına gelir, yani π / 2 <θ ≤ π veya 90 ° <θ ≤ 180 °. Bu nedenle açı geniştir.